Numerieke methoden voor grote lineaire algebraische stelsels
(wi4010)
- De cursus is ingeroosterd in de periode: 7 Februari tot 25
Maart, 2005
Maandag 13.45-15.30 zaal: G Mekelweg 4
Donderdag 15.45-17.30 zaal: G Mekelweg 4
-
Het
collegedictaat is alleen in electronische
vorm beschikbaar.
- Colleges
-
Practische opgaven en de gebruikte programma's in een
zip
of in een
tar
bestand
- Matlab implementatie
van de algorithmen, die beschreven worden in het collegedictaat.
- Historische opmerkingen
-
Rampen veroorzaakt door numerieke fouten.
- Aanvullende
informatie
toepassingen,
rampen veroorzaakt door numerieke fouten, boeken, software pakketten
etc.
-
Blackboard
Numerieke methoden voor grote lineaire algebraische
stelsels
(wi4010)
De cursus start met een korte introduktie van basis lineaire algebra kennis.
Daarna worden directe methoden besproken voor het oplossen van grote
(ijle) lineaire stelsels. De stelsels worden afkomstig gedacht van
gediscretizeerde partiele differentiaal vergelijkingen.
Bij de behandeling van de directe
methoden wordt veel aandacht besteed om de oplossing stabiel te
berekenen ten opzichte van afrondfouten. Afhankelijk van de eigenschappen
van de matrix kunnen de directe methoden verder geoptimalizeerd
worden. Voorbeelden hiervan zijn: Choleski decompositie voor
symmetrische positief definiete matrices, ijle matrix methoden
voor matrices die slecht enkele niet nul elementen bevatten per rij,
band methoden voor band matrices enzovoorts.
Veel praktische problemen geven aanleiding tot kleinste kwadraten
problemen. Enkele methoden om deze problemen op te lossen worden beschreven.
Verder wordt het gedrag ten opzichte van afrondfouten onderzocht.
De cursus wordt afgesloten met een hoofdstuk over iteratieve
methoden voor grote lineaire stelsels vergelijkingen.
We starten met de standaard iteratieve methoden: Gauss Jacobi,
Gauss Seidel en blok varianten hiervan. Daarna bespreken we
de Chebyshev versnellings methode en eindigen met de
geconjugeerde gradienten methode. Voor de geconjugeerde gradienten
methode worden enkele preconditionerings methoden gegeven.
Enkele historische opmerkingen worden gegeven in de volgende
pagina.
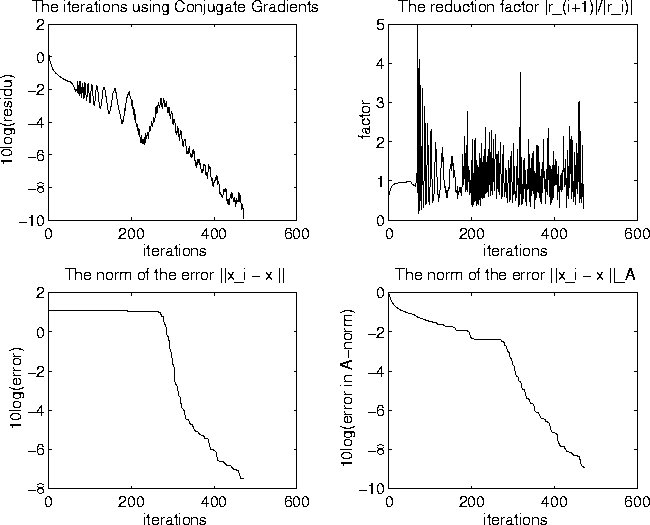
Als voorbeeld laten we het convegentie gedrag zien van de CG methode
voor een buigende balk probleem.

Contact information:
Kees Vuik
Back to
home page or
educational page of Kees Vuik


![]()
![]()