Platform for
Computational
Science and Engineering
Introduction
Computational Science and Engineering (CSE) is a rapidly growing
multidisciplinary area with connections to the sciences, engineering,
mathematics and computer science. CSE focuses on the development of
problem-solving methodologies and robust tools for the solution of
scientific and engineering problems. We believe that CSE will play an
important if not dominating role for the future of the scientific
discovery process and engineering design.
Below we give a more detailed description of Computational Science and
Engineering.
For more information we refer to the
Society for
Industrial and Applied Mathematics (SIAM)
In CSE we deal with the simulation of processes, as they occur amongst
others in the
engineering, physical and economic sciences.
Examples of application areas are fluid dynamics (the aerodynamics of
cars
and aircrafts, combustion processes, pollution spreading), semi-conductor
technology (breeding of cristals, oxidation processes), weather and
climate
prediction (the growing and tracking of tornados, global warming) and
financial mathematics (prediction of stock and option prices).
Simulation is nowadays an equal and indispensable partner
in
the advance of scientific knowledge next to the theoretical and
experimental
research.
It is characteristic for CSE that practical relevant results
are achieved by combining methods and research results from different
scientific areas.
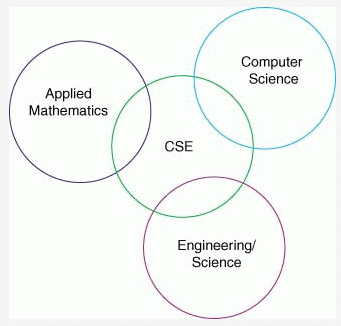
The application area brings the typical problem-dependent know-how,
the knowledge to formulate the problem and model and
to verify the computed results by means of real experiments.
Applied mathematics deals with the definition of a mathematical model,
existence and uniqueness results and
develops efficient methods to solve the mathematical model with
a computer.
Computer science typically takes care for the usability, and
programming of
modern computers and designs powerful software packages.
Especially the interplay of the disciplines is necessary for success.
For instance:
it is possible to parallelize a poor mathematical method and
implement it
on a supercomputer, but this does not help us much!
We need much more a continuing development of mathematical models and
numerical algorithms, the transfer of the algorithms into powerful and
user-friendly software, running this on state-of-the-art computers that
steadily increase their performance.
Basically, we can distinguish a number of important steps in simulation:
- Setting up a model.
At the start of each simulation we have the
development of a mathematical model of the process of interest. This
must be
a simplified image of the reality that contains many relevant
phenomena. It
must be formulated such that the model
has a (unique) solution. Often we obtain a
system of (not analytically solvable) differential equations.
- The analytical treatment.
Analytical tools can be used to obtain properties of the solution:
existence, uniqueness, maximum principle etc. Furtermore for simple
problems an analytical solution can be found. In a number of cases
approximate solutions can be derived using an asymptotical approach.
- The numerical treatment.
Since a computer can only handle discrete
numbers,
we have to discretize the model (the equations and the solution
domain), so
that the computer can deal with them.
For the solution of the resulting matrix from the discrete equations,
mathematicians provide efficient methods.
- The implementation.
Next to the choice of computer language and
data
structures, especially the distributed computation is of
major importance.
- The embedding.
The numerical simulation is just one step in the
product
development in industrial applications. Therefore, we need interfaces,
so
that we can link the simulation programme with CAD tools.
Only in this way it is, for example, possible to use aerodynamics car
simulation results on drag coefficients at an early stage into the
design
process.
- The visualisation.
Typically, after a simulation we have huge data
sets
(not only one drag coefficient as in the example above).
Often we need the velocity in the complete flow domain, or one is
interested
for the optimal control of a robot in the path of the robot arm.
We need to present such results with the help of computer graphics,
so visualization is very important.
- The validation.
After long computer times with many many
computations, we
have the result of a simulation. It is of a primary importance to
verify the results obtained.

