Mathematical modeling of wound healing and subsequent scarring
Wietse Boon
Supervisor: D.C. (Daniel) Koppenol, F.J. (Fred) Vermolen
Site of the project: TU Delft
start of the project: May 2013
In November 2013 the
Interim Thesis
and a
presentation
has been given.
The Master project has been finished in June 2014
by the completion of the
Masters Thesis
and a final
presentation
has been given.
For working address etc. we refer to our
alumnipage.
Summary of the master project:
One of the clinical problems regarding severe burns is the development
of hypertrophic scars, which impair the natural topography of the
effected skin region. The burns are classified on a scale of
severeness that was developed by Guillaume Dupuytren (see image 1 and image 2)
into first, second and third degree burns. The problem of a disturbed
topography plays an important role in second and third degree burns (see
image 3). During the healing of a burn, many complicated biological
processes occur, and one of them is that fibroblasts (see picture 4)
from the surrounding skin regions or from the fat region migrate into
the damaged region, where they partly differentiate into
myo-fibroblasts, and regenerate the extra cellular matrix which supports
the skin tissue. Besides the regeneration of extra cellular matrix, the
(myo-)fibroblasts contract, by which they induce an adjusted
strain-pattern in the damaged region and its surroundings.
The extra cellular matrix, roughly consisting of fibres, in undamaged
skin regions is ordered in a random way with very large orientational fluctuations
over small distances. In the post-damaged region,
however, the randomness of the arrangement of the fibres after repair of
the damage, is much smaller and thereby this arrangement is very
non-isotropic.
This project deals with the mathematical modeling of the development of the
orientation of the fibres in relation to the present fibroblasts.
Migration of fibroblasts is simulated on a cell-level where the migration
of each individual fibroblast is modeled autonomously. In the migration
of the cells, mechanical and chemical stimuli are incorporated, as well
as a stochastic term to mimic local (unknown) fluctuations. The
stochastic term is incorporated via a Wiener process. Further, chemical
and mechanical signals are dealt with by solving reaction-transport
partial differential equations, for which finite-element techniques are
used to have as much as geometrical freedom as possible. We aim at a
quantitative investigation of the biological and physiological factors
that control the isotropy and randomness of the orientation of the
fibroblast-formed post-damage extra cellular matrix.
We will also scrutinize the interaction between the post-damage
fibre orientation and the amount of contraction, where
the latter may lead to an impaired skin surface topography.

Figuur 1: Guillaume Dupuytren

Figuur 2: Classification of the degree of a burn
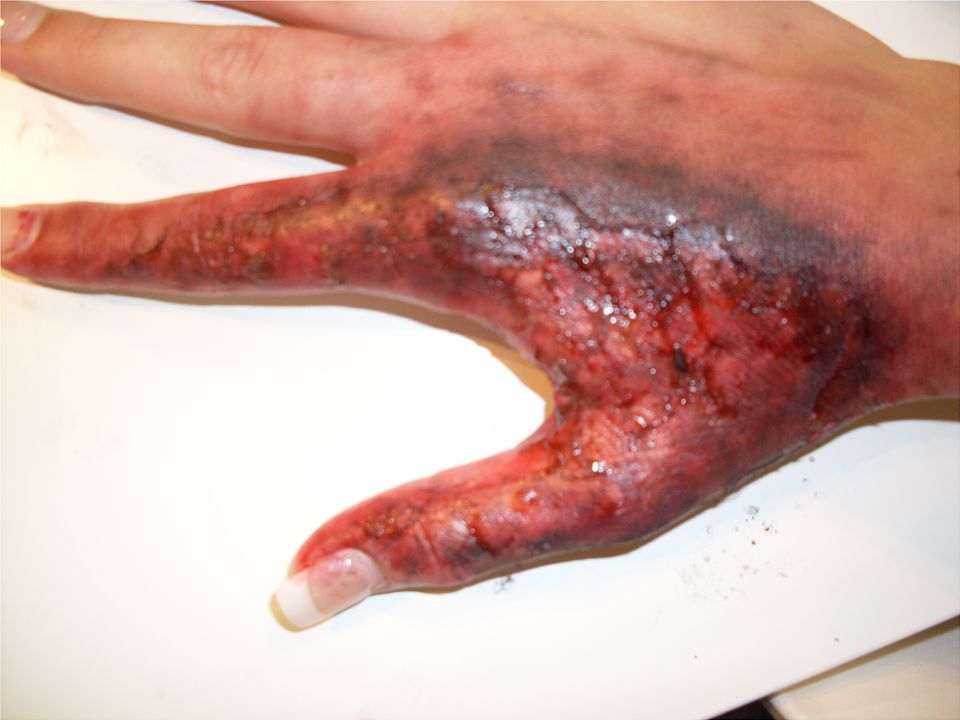
Figuur 3: Third degree burn
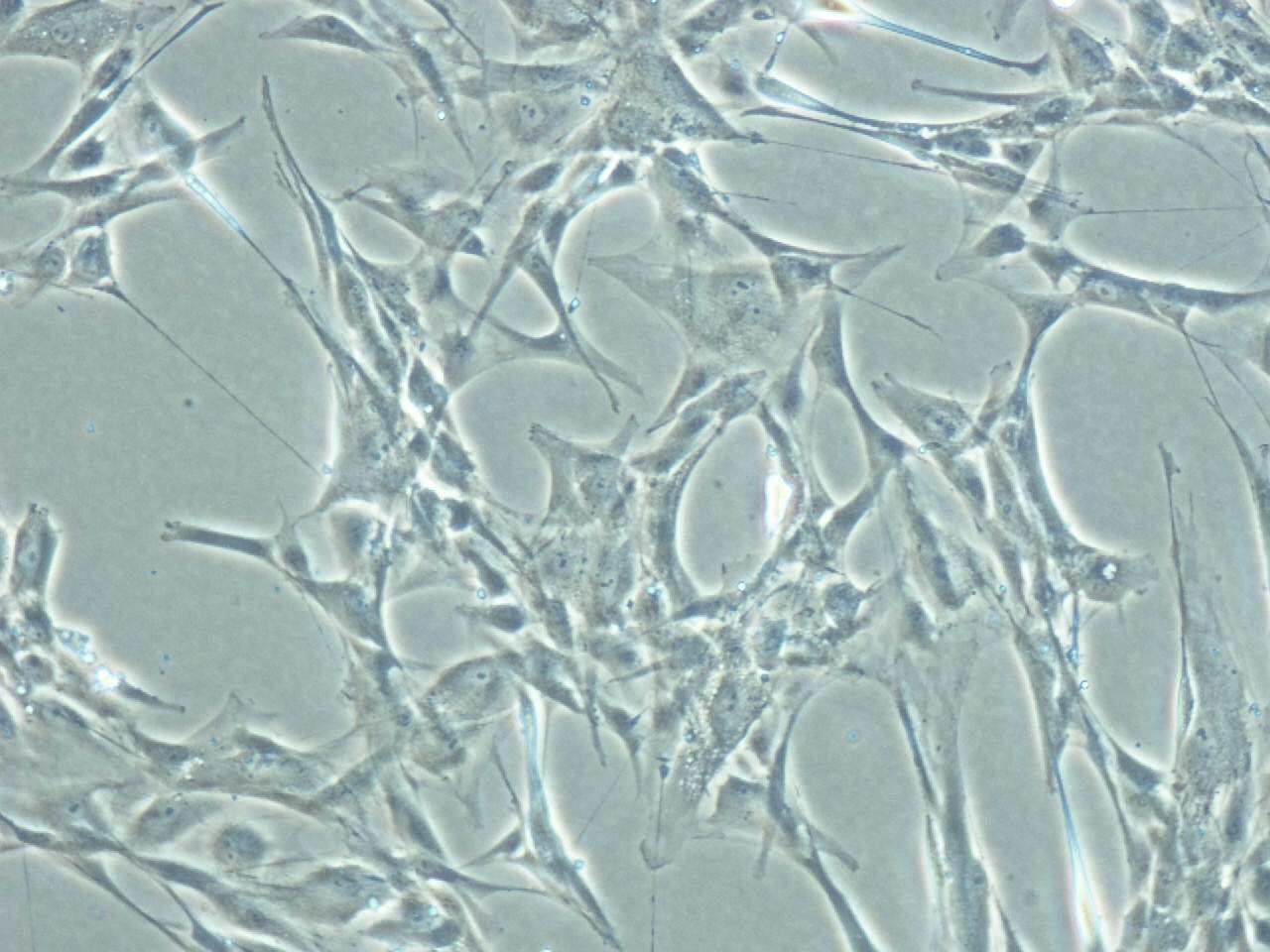
Figuur 4: Fibroblasts

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik



![]()
![]()