Master project of Karl Kästner
Computing the Energy Levels of a Confined Hydrogen Atom
Student:
Karl Kästner
(COSSE student, double degree with
KTH Stockholm)
In March 2012 the
Interim Thesis
and a
presentation has been given.
The Master project has been finished in August 2012
by the completion of the
Masters Thesis
and a final
presentation
has been given.
For working address etc. we refer to our
alumnipage.
Summary of the master project:
The confined one-electron atom is a popular model in theoretical chemistry
and solid-state physics. In most studies, the simplest model of the spherical
confinement is treated. The advantage of the spherical confinement model
is that analytical expressions are known for the wave functions. However,
in many physical situations the spherical confinement model is not realistic.
In this study we consider a model for a hydrogen atom that is confined
in a box. The energy levels of the hydrogen atom can be computed from
the (non-dimensional) Schrödinger equation
In this equation, 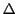 is the Laplace operator,
is the Laplace operator, 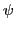 is the wave function,
is the wave function, 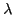 the energy level, and
the energy level, and 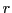 the distance to the centre of mass. This equation is
complemented by homogeneous boundary conditions. Equation 1 plus boundary
conditions form an eigenvalue problem, in which
the distance to the centre of mass. This equation is
complemented by homogeneous boundary conditions. Equation 1 plus boundary
conditions form an eigenvalue problem, in which 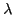 is the eigenvalue and
is the eigenvalue and
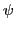 the eigenfunction.
the eigenfunction.
Discretisation of 1 leads to an algebraic eigenvalue problem of the form
For realistic calculations, the size of this matrix can be prohibitive.
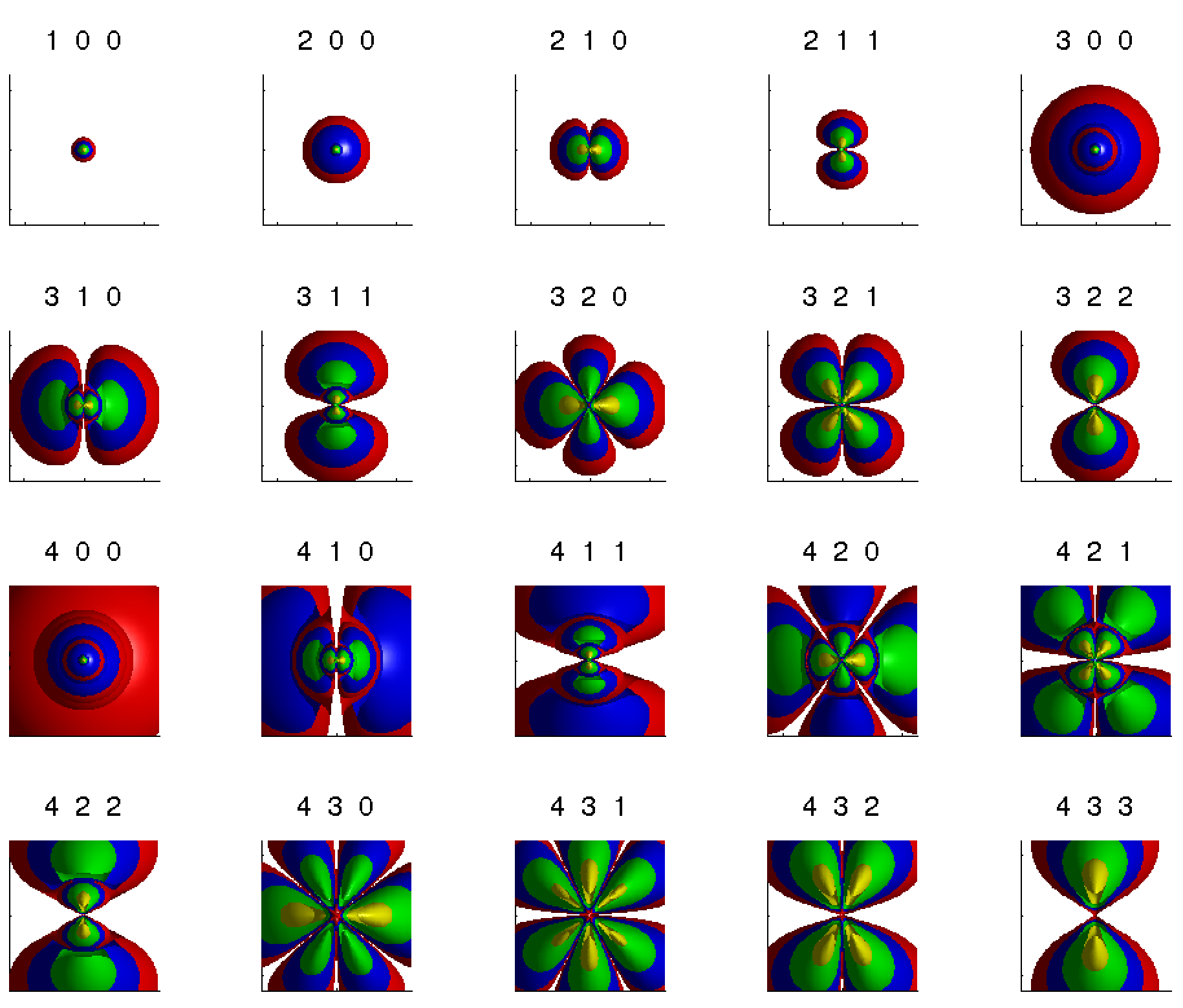
Hydrogen Wave Functions
The main research question is how to compute accurate approximations of
a reasonable number of the smallest analytical eigenvalues 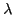 . To this end
the following aspects will be studied:
. To this end
the following aspects will be studied:
- Discretisation with the Finite Difference method.
Specific research questions are:
- What is an optimal scaling of the parameters?
- How should the singularity at
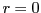 be taken into account?
be taken into account?
- What is the order of convergence of the eigenvalues?
- Solution algorithms for the algebraic eigenvalue problem.
We will consider the following two iterative solution algorithms for
solving the eigenvalue problem: Lanczos method and Jacobi-Davidson
method. Specific research questions are:
- Lanczos: What is the problems size that can be handled. How
reliable are the computed eigenvalues? Can the robustness of the
algorithm be improved, for example by selective reorthogonalisation?
- Jacobi-Davidson: What is the problem size that can be handled?
How reliable are the computed eigenpairs? What is a good preconditioner
for this problem?
- Implementation
An initial implementation will be made using Matlab, with which the
above research questions will be studied. Based on the outcomes of
this study an algorithm will be selected for implementation on a GPU.
Specific research questions are:
- Which algorithm is most promising?
- How can this algorithm be efficiently implemented on a GPU?
- How reliable are the computations?
- Evaluation
The final stage of the research is the evaluation of the
software. This stage will evaluate to what extend the main research
question has been answered: which realistic problems can be solved
with the developed software?
The research will be carried out at the TU Delft, in close collaboration
with the European Space Research and Technology Centre (ESTEC),
located in Noordwijk.

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik

![]() . To this end
the following aspects will be studied:
. To this end
the following aspects will be studied:
![]()
![]()