Berekening van de Energieniveaus van een Vastgepind Waterstofatoom
Student:
Karl Kästner
(COSSE student, double degree met
KTH Stockholm)
In maart 2012 is de
scriptie
verschenen en een
presentatie gegeven.
De afstudeeropdracht is in augustus 2012 afgerond met het schrijven van
het
afstudeerverslag
en het geven van de
afstudeervoordracht.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Het vastgepinde waterstofatoom is een populair model in de theoretische scheikune
en vastestoffysica. In de meeste onderzoeken, wordt het eenvoudigste model van de
bolvormige opsluiting behandeld.
Het voordeel van de bolvormige opsluiting is dat er anlytische bekend
zijn voor de golffuncties. Echter in veel fysische situaties is dit model niet realistisch.
In dit onderzoek beschouwen we een model voor een waterstofatoom, dat
vastgepind is in een kubus. De energieniveaus van het waterstofatoom
kunnen bepaald worden uit de
(dimensieloze) Schrödinger vergelijking
In deze vergelijkingt, is 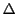 de Laplace operator,
de Laplace operator, 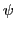 de golffunctie,
de golffunctie, 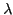 het energieniveau en
het energieniveau en 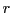 de afstand tot het centrum van de massa. Deze vergelijking
wordt gecomplementeerd met randvoorwaarden.
Vergelijking 1 plus randvoorwaarden vormt een eigenwaardeprobleem, waarin
de afstand tot het centrum van de massa. Deze vergelijking
wordt gecomplementeerd met randvoorwaarden.
Vergelijking 1 plus randvoorwaarden vormt een eigenwaardeprobleem, waarin
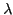 de eigenwaarde is en
de eigenwaarde is en
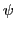 de eigenfunctie.
de eigenfunctie.
Discretisatie van 1 leidt tot een algebraisch
eigenwaarde probleem van de vorm
Voor realistische berekeningen is de afmeting van de matrix erg groot.
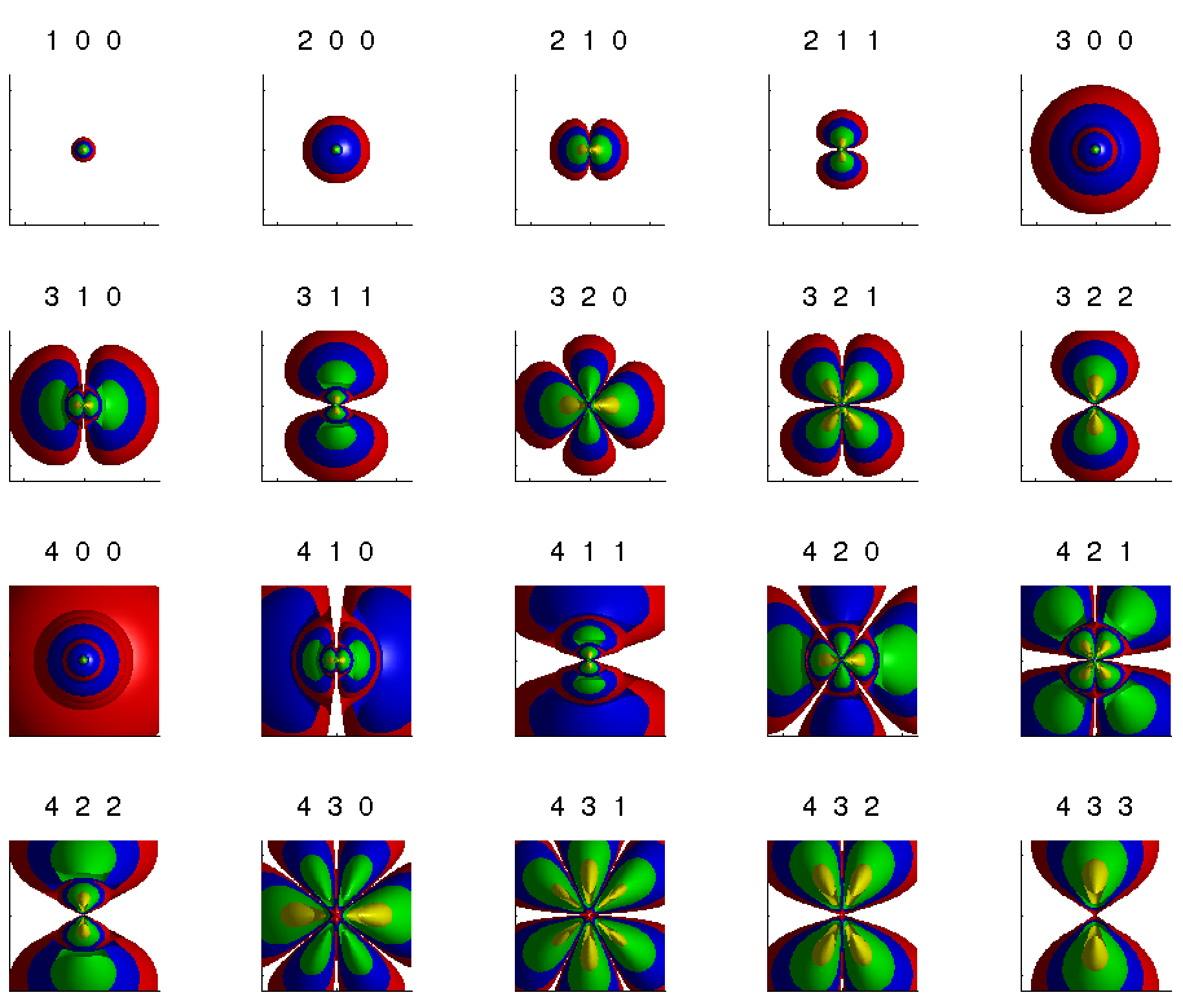
Waterstof Golffuncties
De hoofd onderzoeksvraag is het efficient bepalen van nauwkeurige benaderingen
van een redelijk aantal kleinst eigenwaarden
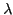 . Om deze vraag te beantwoorden zullen de volgende
onderwerpen bestudeerd worden:
. Om deze vraag te beantwoorden zullen de volgende
onderwerpen bestudeerd worden:
- Discretizatie met de eindige differentie methode.
Specifieke onderzoeksvragen zijn:
- Wat is een optimale schaling van de parameters?
- Hoe moet de singulariteit op
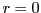 behandeld worden?
behandeld worden?
- Wat is de orde van de convergentie van de eigenwaarde benaderingen?
- Een algorithme voor het oplossen van het eigenwaardeprobleem.
We zullen de volgende iteratieve algorithmen beschouwen voor het oplossen van het
eigenwaardeprobleem:
de Lanczos methode en de Jacobi-Davidson methode.
Specifieke onderzoeksvragen zijn:
- Lanczos: Wat is de maximale probleemgrootte? Hoe betrouwbaar zijn de
berekende eigenwaarden?
Kan de robuustheid van het algorithme verbeterd worden, bijvoorbeeld
door selectieve reorthogonalisatie?
- Jacobi-Davidson:
Wat is de maximale probleemgrootte? Hoe betrouwbaar zijn de
berekende eigenwaarden?
Wat is een goede
preconditioner voor dit probleem?
- Implementatie
Om de onderzoeksvragen te bestuderen zal er een eenvoudige implementatie
gemaakt worden in Matlab. Afhankelijk van de uitkomsten
van deze studie, zal er een algorithme geselecteerd worden
voor implementatie op een GPU.
Specifieke onderzoeksvragen zijn:
- Welk algorithme is het meest veelbelovend?
- Hoe kan dit algorithme efficient geimplementeerd worden op een GPU?
- Hoe betrouwbaar zijn de berekeningen?
- Evaluatie
De laatste stage van het onderzoek is de evaluatie van de software.
Hierin zal geevalueerd worden in hoeverre de hoofd onderzoeksvragen
beantwoord zijn.
Het onderzoek zal uitgevoerd worden aan de TU Delft in nauwe samenwerking
met de European Space Research and Technology Centre (ESTEC),
gevestigd in Noordwijk.

Contact informatie:
Kees
Vuik

Terug naar de
home page
of de
afstudeerpagina van Kees Vuik

![]() . Om deze vraag te beantwoorden zullen de volgende
onderwerpen bestudeerd worden:
. Om deze vraag te beantwoorden zullen de volgende
onderwerpen bestudeerd worden:
![]()
![]()