Modelling Phase Transformations in Steel Alloys
Mathias Mul
(COSSE student, double degree with
TU Berlin)
Supervisor: Fred Vermolen
Site of the project:
Tata Steel
Breedbandweg 1
1951 MC Velsen-Noord
Supervisor Tata Steel: Kees Bos
start of the project: November 2013
In May 2014 the
Interim Thesis
has appeared
and a
presentation
has been given.
The Master project has been finished in September 2014
by the completion of the
Masters Thesis
and a final presentation
has been given.
For working address etc. we refer to our
alumnipage.
Summary of the master project:
The mechanical properties of steel are determined by its composition and
microstructure. There are many ways to adapt the microstructure of steel
alloys. Thermal treatment is widely used to give steel its properties
for specific purposes. Effects on the internal structure of a steel
alloy under cooling or heating can be modelled on micro scale. The
average grain size is the most interesting microstructure parameter,
because it has been extensively correlated to mechanical properties.
An explanation for the different behaviour lies within the
transformation of the iron lattice from face centred cubic (fcc) at
higher temperatures to body centred cubic (bcc) at lower temperatures.
The high temperature phase is referred to as austenite and the low
temperature phase is referred to as ferrite. Therefore, the phase change
from fcc to bcc is also called austenite-ferrite transformation. (image
below)
Steel consists mainly of the elements iron (Fe) and carbon (C). The
movement of the interface between austenite and ferrite depends partly
on the carbon concentration at the interface. Ferrite is saturated with
carbon at much lower concentrations than austenite. Therefore, during
the transformation, carbon is pushed ahead of the moving interface. This
can be modelled by the diffusion equation, which mathematically
describes carbon spreading through the austenite. (image below)
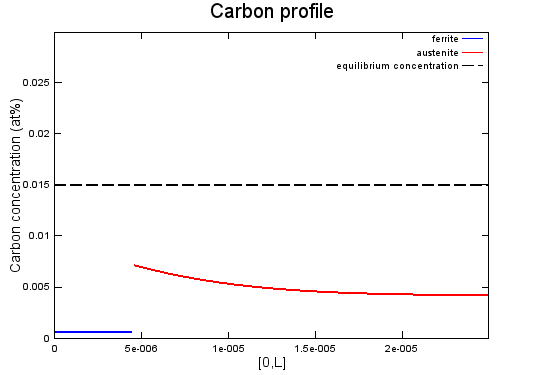
The goal of this thesis is to model grain growth of different phases in
an accurate and efficient way. This can be done using Cellular Automata
(CA) models. A CA model is a discrete model with a regular grid of
cells. Each cell has a set of properties, most importantly its state,
neighbourhood, and transformation rule. Given an initial state, each
time step the state of a cell is updated by a rule that usually is a
mathematical function of the states of its neighbours.

Results of simulations to estimate the stability of the interface.

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik



![]()
![]()