IDR(s) revisited
Marijn Schreuders
Supervisor: Martin van Gijzen
Site of the project: TU Delft
start of the project: November 2013
In February 2014 the
Interim Thesis
and a
presentation
has been given.
Summary of the master project:
Suppose we want to solve a linear system of equations. In 1980 the IDR
method was first proposed by Peter Sonneveld to solve such a system. IDR
stands for Induced Dimension Reduction. The underlying idea is that the
residuals are forced to be in subspaces of reducing dimension.
IDR has been long been overshadowed by Bi-CG-type methods and GMRES-type
methods, although the underlying mathematical ideas are totally
different. In recent years there has been renewed interest in IDR and in
2007 Peter Sonneveld and Martin van Gijzen proposed an extension to IDR
called IDR(s). From practical experience we see that the IDR(s) method can
perform very well compared in certain situations (see the Figure below).
It turns out that IDR(s) can be seen in the framework of projection
methods. A projection method is an iterative method that searches for an
approximate solution in a Krylov subspace such that it is orthogonal to
another Krylov subspace. One goal of this research is to find out how
exactly we can see IDR(s) in this framework. Here we follow Valeria
Simoncini and Daniel B. Szyld in their paper 'Interpreting IDR as a
Petrov-Galerkin method'.
In this same paper Simoncini and Szyld propose a new version of IDR,
called Ritz-IDR. For the omega's, one of the parameters in the IDR(s)
algorithm, they use the reciprocals of some of the approximations of the
eigenvalues (called Ritz values) of the matrix. They generate these Ritz values by
using a small number of iterations of a Krylov subspace method for
eigenvalue problems, such as the Arnoldi method. However, IDR(s) can also
be used to generate Ritz values. Hence, our second goal will be to use
IDR(s) itself to generate the Ritz values.
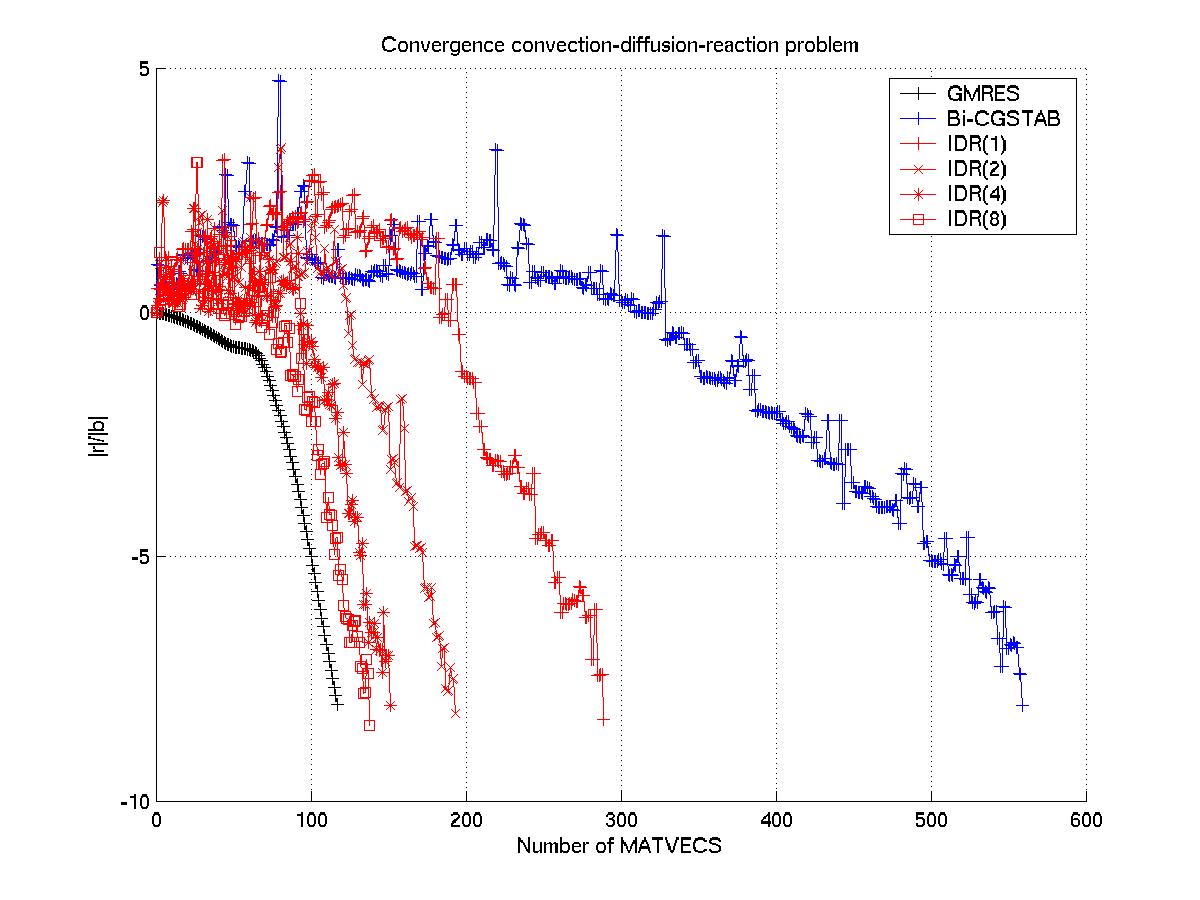
Convergence of various Krylov subspace methods.

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik

![]()
![]()