Een nieuwe kijk op IDR(s)
Marijn Schreuders
Dagelijks begeleider: Martin van Gijzen
Plaats van afstuderen: TU Delft
start van afstuderen: november 2013
In februari 2014 is de
scriptie
verschenen en een
presentatie
gegeven.
Korte omschrijving van de afstudeeropdracht:
Voor het oplossen van een lineair stelsel vergelijking zijn
verschillende methoden beschikbaa.
In 1980 is de IDR methode bedacht door Peter Sonneveld om zo'n stelsel
op te lossen. IDR betekent Induced Dimension Reduction. Het
onderliggende idee is dat de residuen element zijn van deelruimten, die
een steeds kleinere afmeting krijgen.
IDR is lang overschaduwd door Bi-CG-type methoden en GMRES-type
methoden. De mathematische principes voor IDR zijn compleet verschillend
van de andere methoden.
Onlangs is er opnieuw interesse in de IDR methode onstaan en in 2007
hebben Peter Sonneveld en Martin van Gijzen een uitbreiding bedacht van
IDR genaamd IDR(s). Het blijkt dat IDR(s) veel sneller kan convergeren
dan de andere methode, zie onderstaande figuur.
Het blijkt dat IDR(s) gezien kan worden als een projectie methode. Een
projectie methode is een iteratieve methode die een benadering zoekt
in een Krylov deelruimte zo dat de fout loodrecht staat op een andere
Krylov deelruimte. Een doel van dit onderzoek is hoe IDR(s) gezien kan
worden als een projectie methode?
In dit onderzoek volgen we Valeria
Simoncini en Daniel B. Szyld in hun artikel 'Interpreting IDR as a
Petrov-Galerkin method'.
In hetzelfde paper geven Simoncini en Szyld een nieuwe versie van IDR,
genaamd Ritz-IDR. Voor de omega's, een van de parameters in IDR(s)
nemen ze de inverse van de Ritzwaarden van de matrix. Ze maken deze
Ritzwaarden door het doen van een klein aantal iteraties van een Krylov
deelruimte methode voor het benaderen van eigenwaarden, bijvoorbeeld de
Arnoldi methode. Echter IDR(s) kan ook gebruikt worden om Ritzwaarden te
bepalen. Het tweede doel is dan ook om te zien of IDR(s) gebruikt kan
worden voor het bepalen van de Ritzwaarden.
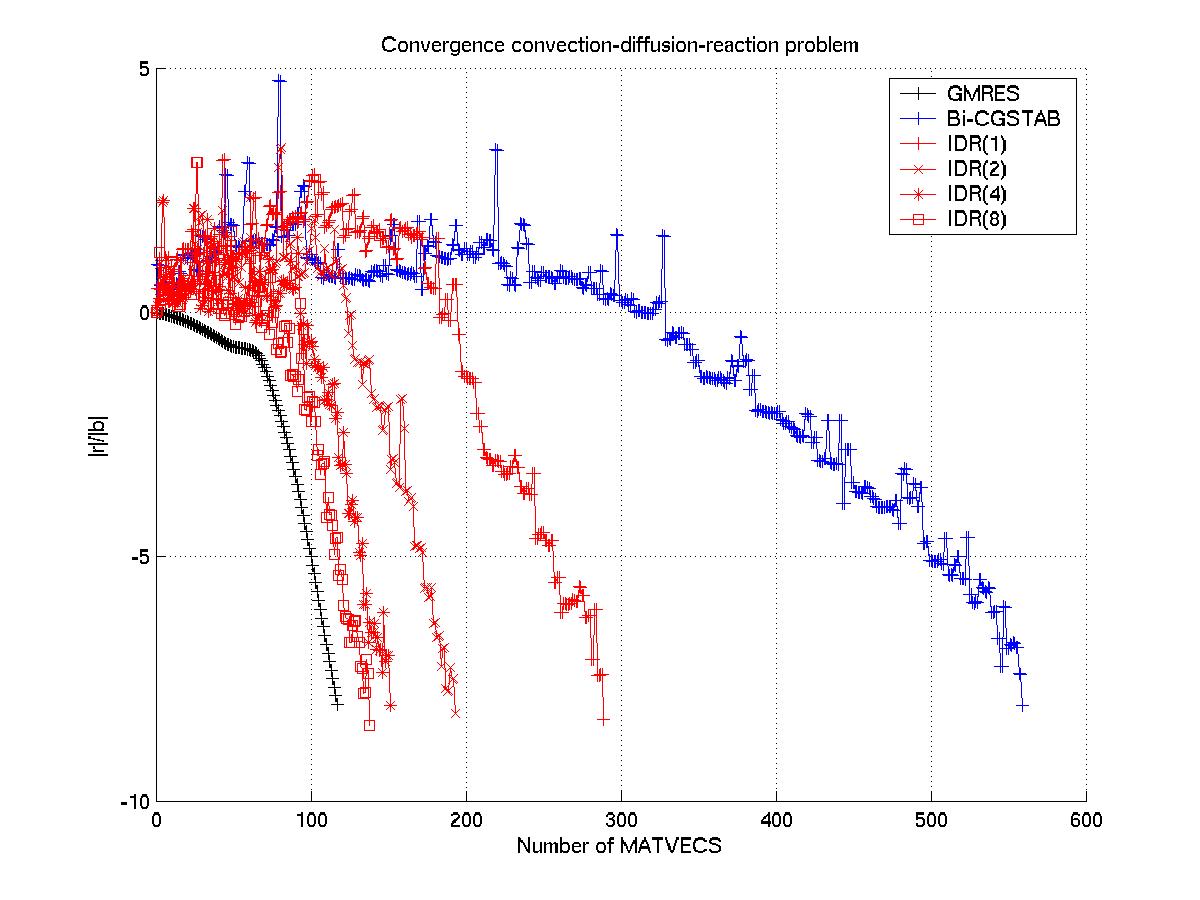
Convergentie van verschillende Krylovdeelruimte methoden.

Contact informatie:
Kees
Vuik

Terug naar de
home page
of de
afstudeerpagina van Kees Vuik

![]()
![]()