Het efficient oplossen van de Helmholtz vergelijking
Jok Tang
Plaats van afstuderen:
Shell
Hoekstede Building
Visseringlaan 26
2280AB Rijswijk
start van afstuderen: november 2003
In februari 2004 is de
scriptie
verschenen.
De afstudeeropdracht is in augustus 2004 afgerond met het schrijven van
het
afstudeerverslag.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Het efficient oplossen van de Helmholtz vergelijking op erge grote roosters
(1000 x 1000 x 1000) is van groot belang voor Shell en een uitdaging voor
numerieke lineaire algebra onderzoek.
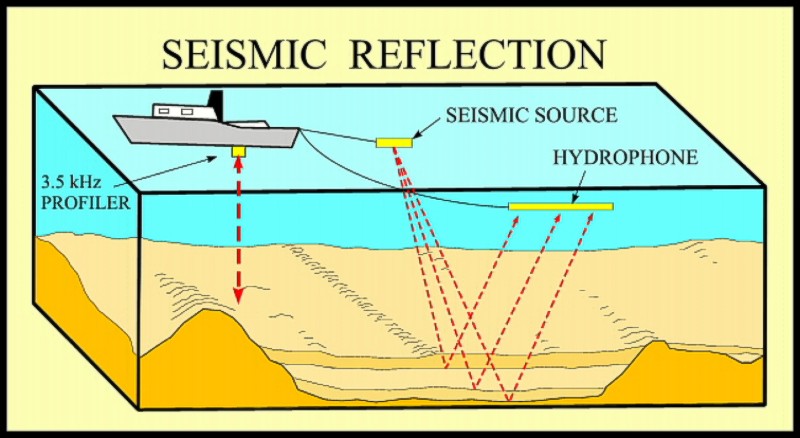
Deze vergelijking speelt een rol bij het seismisch onderzoek van de aardkorst.
Dit onderzoek wordt gebruikt om de verschillende aardlagen in beeld te brengen,
waarna geschikte plaatsen voor het vinden van olie en gas bepaald kunnen
worden.

Op dit moment zijn er een aantal
oplosmethoden bekend:
- ILU preconditioners
- multigrid preconditioners
- shifted Laplace preconditioners
- separation of variable preconditioners
- Gander and Nataf preconditioners
Sommige preconditionering werken goed voor bepaalde applicaties, maar falen
voor andere toepassingen (waarvan sommige, die voor Shell van belang zijn).
Gedurende het afstuderen zal een literatuurstudie gedaan worden van de
mogelijke oplosmethoden. Daarna zal een vergelijking plaatsvinden van de
verschillende methoden voor realistische toepassingen.
Het onderzoeken van de eigenschappen van de methoden is van belang om te kunnen
begrijpen waarom de methoden niet werken. Mogelijk moet er een combinatie van
bovenstaande methoden gebruikt worden.
De volgende punten zullen aan de orde komen:
-
een vergelijking van methode 3 en 4 voor realistische 3D problemen,
- onderzoek van de eigenwaarden van methode 3 en 4. Voor methode 3 zijn
enkele ideeen beschikbaar. Kunnen deze ideeen bewezen worden? Numerieke
experimenten kunnen daar bij helpen.
- Het blijkt dat methode 3 goede eigenschappen heeft voor grote
eigenwaardecomponenten, maar slechte eigenschappen voor kleine
eigenwaardecomponenten. Als een van de andere methoden snel convergeert voor de
kleine eigenwaarden dan kan een combinatie mogelijk goede resultaten geven.
- onderzoek van continuering. Mogelijkheden: verhoog k, of verklein de
stapgrootte of verklein de artificiele demping etc.

Contact informatie:
Kees
Vuik

Terug naar de
home page
of de
afstudeerpagina van Kees Vuik


![]()
![]()