(Parallelle) Solvers voor de CFD-code WISH3D (
figuren)
E.H. Tazammourti
Plaats van afstuderen:
TNO Technisch Physische Dienst
Stieltjesweg 1 (Postbus 155)
2600 AD Delft
start van afstuderen: augustus 1996
De afstudeeropdracht is juni 1997 afgerond met het schrijven van het
afstudeerverslag.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Deze omschrijving is voortgekomen uit het literatuur onderzoek voor mijn
afstudeerwerk bij TNO-TPD-TU Delft. Binnen de Procesfysica afdeling worden
stromingsproblemen, afkomstig van onder andere industriele procesovens,
uitgerekend met behulp van WISH3D. WISH3D, ontwikkeld bij TNO-TPD, is
een CFD (Computational Fluid Dynamics) model voor het simuleren van
stromingen, warmteoverdracht en transport van chemische stoffen.
WISH3D heeft twee hoofdonderdelen:
1. Het mathematische model voor het beschrijven van fysische problemen.
Dit model heeft de vorm van een aantal gekoppelde stelsels lineaire
vergelijkingen verkregen door het discretiseren van niet-lineaire
partiele differentiaalvergelijkingen (PDV) met behulp van een eindige
volume methode.
2. Het numerieke model voor het oplossen van de gediscretiseerde
vergelijkingen met behulp van WISH3D solvers.
Het doel van het afstudeeronderzoek is om een aantal Krylov solvers in
WISH3D in te bouwen en uit te zoeken of deze solvers een beter
convergentiegedrag kunnen opleveren dan de huidige WISH3D solvers aan de
hand
van testproblemen.
In de scriptie worden de volgende onderwerpen behandeld:
De mathematische beschrijving van compressibele turbulente stromingen.
Hierbij worden een aantal partiele differentiaalvergelijkingen kort
geformuleerd, die gebaseerd zijn op de behoudswetten van de klassieke
fysica, aangevuld met de toestandsvergelijking voor een ideaal gas. Voor
het beschrijven van de turbulente kinetische energie en de dissipatie ervan,
wordt er gebruik gemaakt van het standaard (k-epsilon) model. De partiele
differentiaalvergelijkingen worden aangevuld met begin- en randvoorwaarden.
De randvoorwaarden voor de kinetische energie en de dissipatie ervan worden
opgelegd met behulp van de zogenaamde wandfuncties.
Het discretiseren van de gegeven partiele differentiaalvergelijkingen met
behulp van een eindige volume methode. Hieruit worden stelsels lineaire
vergelijkingen verkregen van de vorm Ax = b, waarbij A een sparse matrix is.
De vector x bevat de onbekende elementen afkomstig van een snelheidscomponent,
enthalpie (temperatuur), turbulente kinetische energie of dissipatie van de
turbulente kinetische energie. Voor het bepalen van een stelsel vergelijkingen
voor de druk wordt een druk-correctie methode, SIMPLE, gebruikt.
Het beschrijven van een aantal van de huidige WISH3D solvers. Deze zijn
Gauss-Jacobi, Gauss-Seidel, S.O.R.,Line-TDMA en Plane-TDMA. Dit zijn
iteratieve oplosmethoden voor lineaire stelsels vergelijkingen. De beschrijving
hiervan is gebaseerd op het boek van Patanker [ Numerical Heat Transfer and
Fluid Flow ].
Korte beschrijving van een aantal Krylov deelruimte methoden. Deze methoden
zijn de Geconjugeerde Gradienten methode (CG), de CG methode toegepast op de
normaal vergelijkingen A'Ax = A'b of AA'y = b met A'y = x, twee varianten van
de Bi-CG methode: CGS en Bi-CGSTAB en twee varianten van Krylov methoden met
lange recurrenties: GCR en GMRES. Deze methoden dienen als nieuwe
solvers aan WISH3D te worden toegevoegd.
De scriptie wordt afgesloten met het presenteren van een voorstel
voor de afstudeerfase.

A regenerative cross-fired glassmeltoven.
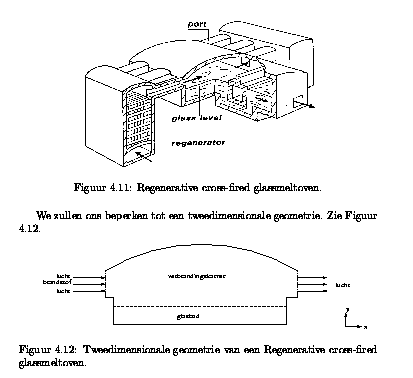
De geometrie van een glassmeltoven.
Er zijn een aantal testen uitgevoerd met de nieuwe solvers op de
bovenstaande glassmeltoven. Hieronder worden de uiteindelijke resultaten
getoond van deze simulaties.
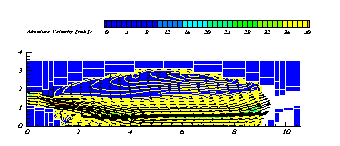
De snelheid in het z-vlak van de glassmeltoven.
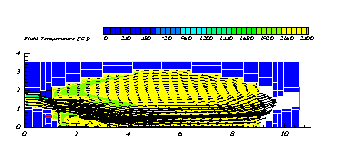
De temperatuur in het z-vlak van de glassmeltoven.
Contact information:
Kees Vuik
Back to
home page
or
Afstudeer pagina
of Kees Vuik
![]()
![]()


