Limiting discontinuous-Galerkin met gebruik van wavelets
Thea Vuik
Afstudeerhoogleraar: Prof.dr.ir. A.W. Heemink
Dagelijks begeleider: Jennifer K. Ryan
Plaats van afstuderen: TU Delft
start van afstuderen: december 2011
In maart 2012 is de
scriptie
verschenen en een
presentatie gegeven.
De afstudeeropdracht is in augustus 2012 afgerond met het schrijven van het
afstudeerverslag
en het geven van de
afstudeervoordracht.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Om de Discontinue Galerkin methode (DG) efficient toe te passen op hyperbolische problemen die schokken laten ontstaan, worden limiting technieken gebruikt. Hierdoor verminderen de verkeerde oscillaties in de buurt van discontinuiteiten.
Het behandelen van limiting technieken is van belang voor allerlei zaken als klimaatmodellering, ondiep-water vergelijkingen en numerieke stromingsleer. Hoewel er vele standaard limiting technieken bestaan, bestaat er geen overeenstemming over het gebruik van een passende limiting procedure voor multidimensionale berekeningen.
Er zijn twee moeilijkheden wat het gebruik van limiting betreft:
- Het vinden van de discontinuiteit zelf; vooral multidimensionaal is dat erg lastig;
- Het behouden van hoge nauwkeurigheid op afstand van de schok.
In dit project wordt geprofiteerd van de vele vrijheidsgraden die bij DG mogelijk zijn voor iedere tijdsstap. Daarnaast wordt een Multi Resolutie Analyse (MRA) gebruikt om de DG benadering te limiten. Hoewel dit idee vergelijkbaar is met eerdere procedures (de gebruikte coefficienten voor benadering worden aangepast), worden hierbij technieken van wavelet analyse gebruikt. Deze ideeen worden lokaal geimplementeerd in gebieden waar limiting nodig is, in plaats van gebruik te maken van de standaard total variation bounded limiter.
DG is een veelbelovend hulpmiddel voor vele onverkende toepassingen, maar het vinden van de juiste limiting procedure vormt een uitdaging. Het nut van het voorgestelde onderzoek is dat onderzoek naar de oplossingsruimte (bijvoorbeeld niet-polynomen en waveletachtige bases) in deze gebieden ruimte laat voor ontwikkeling van limiting procedures voor DG.
Daarnaast is het mogelijk dat op deze manier een nieuw, efficienter numeriek hulpmiddel gevonden wordt voor toepassingen als klimaatmodellering, de ondiep-water vergelijkingen en numerieke stromingsleer.
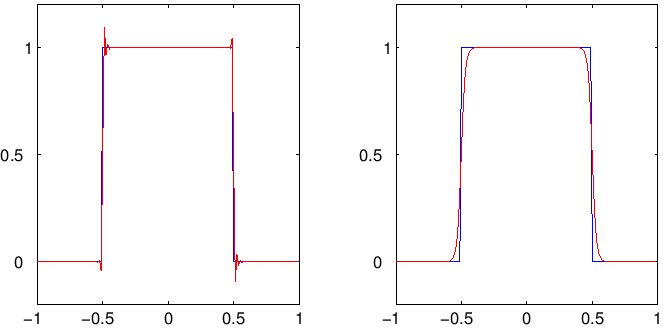
Voorbeeld van een een dimensionale DG oplossing in rood, in vergelijking met de exacte oplossing (blauw) voor een lineaire transportvergelijking met een blokgolf als beginvoorwaarde.
Links: zonder limiting; Rechts: met limiting.
Zonder limiting ontwikkelt DG verkeerde oscillaties in de buurt van discontinuiteiten. Deze limiting technieken kunnen gebruikt worden in ondiep-water modellen.

Voortplanting van golven in de haven van Zeebrugge, Vlaanderen.

Contact informatie:
Kees
Vuik

Terug naar de
home page
of de
afstudeerpagina van Kees Vuik


![]()
![]()