Research Interests

Poisson equation solved on the surface of the teapot
Compressible flow finite element simulation in scramjet geometry
Compressible flow finite element simulation in scramjet geometry
Compressible flow finite element simulation over forward facing step geometry
Double Mach reflection compressible flow finite element simulation
Burgers equation solved in space-time domain
Swirling convective flow
Goal-oriented error estimation and adaptive grid refinement

Finite Element & Isogeometric Analysis

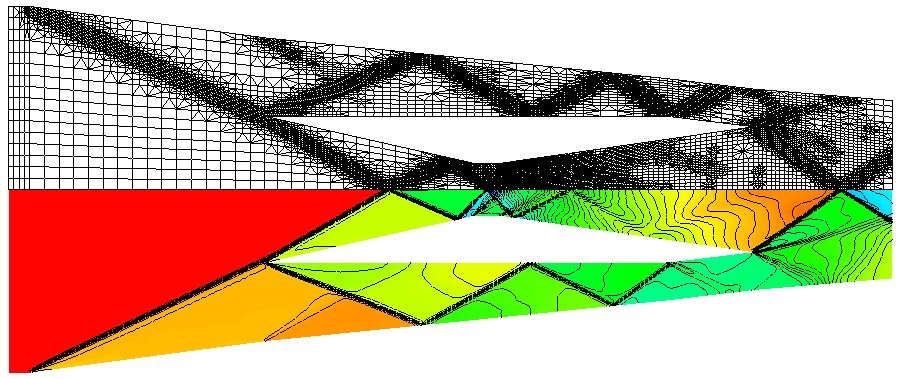
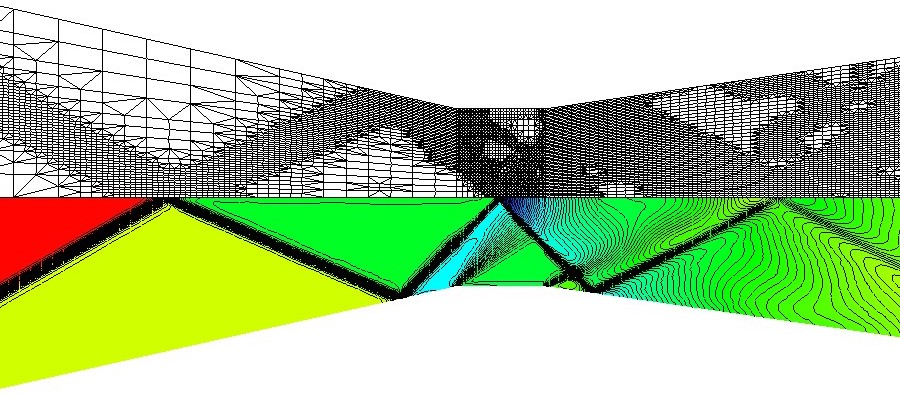
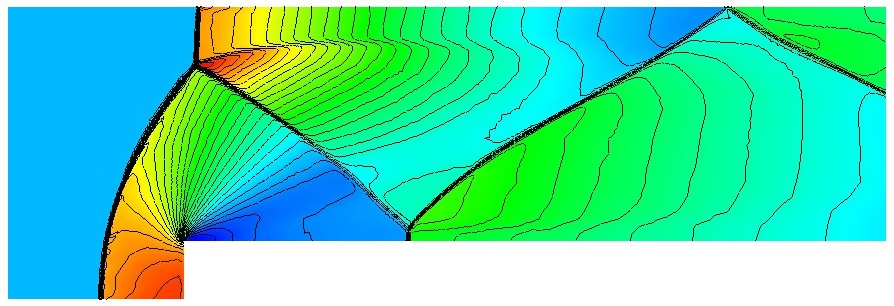
One of my earliests research interests is finite element analysis, where I have developed solvers for steady state as well as time-dependent compressible flows and other types of transport problems that operate on unstructured finite element meshes and use gradient recovery-based error indicators and a posteriori goal-oriented error estimation techniques to steer dynamical mesh adaptation.

I recently shifted my research focus from finite element to isogeometric analysis, which I consider the natural generalization of finite elements to higher-order approximations and more accurate geometry modelling capabilities. Our group is mainly working on the development of isogeometric solvers for different types of flow problems with strong focus on compressible flows in industrial applications.

Most of my research on finite elements was pursued in the open-source software package Featflow2. My research in the field of isogeometric analysis is pursued in the open-source C++ library G+Smo. I am moreover main developed of the Fluid Dynamic Building Block library.

Selected contributions

IGA
  • Merle Backmeyer, Stefan Kurz, Matthias Möller, and Sebastian Schöps. Solving electromagnetic scattering problems by isogeometric analysis with deep operator learning, 2024. [ DOI | http ]
  • Y. Ji, M. Möller, and H. M. Verhelst. Design Through Analysis, pages 303--368. Springer International Publishing, November 2023. [ DOI | http ]
  • Ye Ji, Matthias Möller, Yingying Yu, and Chungang Zhu. Boundary parameter matching for isogeometric analysis using Schwarz-Christoffel mapping. Engineering with Computers, July 2024. [ DOI | http ]
  • H. M. Verhelst, A. Mantzaflaris, M. Möller, and J. H. Den Besten. Goal-adaptive meshing of isogeometric Kirchhoff-Love shells. Engineering with Computers, March 2024. [ DOI | http ]
  • Ye Ji, Kewang Chen, Matthias Möller, and Cornelis Vuik. On an improved PDE-based elliptic parameterization method for isogeometric analysis using preconditioned Anderson acceleration. Computer Aided Geometric Design, 102:102191, 2023. [ DOI ]
  • Ye Ji and Matthias Möller. Mesh Generation for Twin-Screw Compressors by Spline-Based Parameterization Using Preconditioned Anderson Acceleration, pages 77--87. Springer Nature Switzerland, 2024. [ DOI | http ]
  • Jingya Li. A new contact method for Simcenter Madymo: Contact method based on isogeometric analysis, 2023. [ http ]
  • H.M. Verhelst, J.H. Den Besten, and M. Möller. An adaptive parallel arc-length method. Computers & Structures, 296:107300, June 2024. [ DOI | http ]
  • Roel Tielen, Matthias Möller, and Cornelis Vuik. Combining p-multigrid and multigrid reduction in time methods to obtain a scalable solver for isogeometric analysis. SN Appl. Sci., 4(6), June 2022. [ DOI | http ]
  • Miquel Herrera Clapera. High-order discretization of hyperbolic equations: Characterization of an isogeometric discontinuous Galerkin method, 2021. [ http ]
  • Jochen Hinz, Andrzej Jaeschke, Matthias Möller, and Cornelis Vuik. The role of PDE-based parameterization techniques in gradient-based IGA shape optimization applications. Computer Methods in Applied Mechanics and Engineering, 378:113685, 2021. [ DOI | http ]
  • Matthias Möller, Deepesh Toshniwal, and Frank van Ruiten. Physics-informed machine learning embedded into isogeometric analysis. In Mathematics: Key enabling technology for scientific machine learning. Platform Wiskunde, 2021. [ http ]
  • Roel Tielen, Matthias Möller, and Cornelis Vuik. A block ILUT smoother for multipatch geometries in isogeometric analysis. In Carla Manni and Hendrik Speleers, editors, Advanced Methods for Geometric Modeling and Numerical Simulation, volume 49 of Springer INdAM Series, pages 259--278. Springer International Publishing, Cham, 2022. [ DOI ]
  • Hugo H.M. Verhelst, Matthias M. Möller, Henk J.H. Den Besten, Angelos Mantzaflaris, and Mirek M.L. Kaminski. Stretch-based hyperelastic material formulations for isogeometric Kirchhoff-Love shells. Computer-Aided Design, 139:103075, 2021. [ DOI | http ]
  • Jochen Hinz. PDE-based parameterization techniques for isogeometric analysis applications, 2020. [ http ]
  • Jochen Hinz, Michael Abdelmalik, and Matthias Möller. Goal-oriented adaptive THB-spline schemes for PDE-based planar parameterization, 2020. [ arXiv | http ]
  • Jochen Hinz, Jan Helmig, Matthias Möller, and Stefanie Elgeti. Boundary-conforming finite element methods for twin-screw extruders using spline-based parameterization techniques. Computer Methods in Applied Mechanics and Engineering, 361:112740, 2020. [ DOI | http ]
  • Andrzej Jaeschke and Matthias Möller. High-order isogeometric methods for compressible flows. I. Scalar conservation laws. In Harald van Brummelen, Alessandro Corsini, Simona Perotto, and Gianluigi Rozza, editors, Numerical Methods for Flows: FEF 2017 Selected Contributions, pages 21--29, Cham, 2020. Springer International Publishing. [ DOI | arXiv | http ]
  • Matthias Möller and Andrzej Jaeschke. High-order isogeometric methods for compressible flows. II. Compressible Euler equations. In Harald van Brummelen, Alessandro Corsini, Simona Perotto, and Gianluigi Rozza, editors, Numerical Methods for Flows: FEF 2017 Selected Contributions, pages 31--39, Cham, 2020. Springer International Publishing. [ DOI | arXiv | http ]
  • Roel Tielen, Matthias Möller, Dominik Göddeke, and Cornelis Vuik. p-multigrid methods and their comparison to h-multigrid methods within Isogeometric Analysis. Computer Methods in Applied Mechanics and Engineering, 372:113347, 2020. [ DOI | arXiv | http ]
  • Roel Tielen, Matthias Möller, and Kees Vuik. A direct projection to low-order level for p-multigrid methods in isogeometric analysis. In Proceedings of ENUMATH 2019, the 13th European Conferences on Numerical Mathematics and Advanced Applications. Springer-Verlag, 2020.
  • Hugo Verhelst, Matthias Möller, Henk Den Besten, Fred Vermolen, and Mirek Kaminski. Equilibrium path analysis including bifurcations with an arc-length method avoiding a priori perturbations. In Proceedings of ENUMATH 2019, the 13th European Conferences on Numerical Mathematics and Advanced Applications. Springer-Verlag, 2020.
  • Jochen Hinz, Joost van Zwieten, Matthias Möller, and Fred Vermolen. Isogeometric analysis of the Gray-Scott reaction-diffusion equations for pattern formation on evolving surfaces and applications to human gyrification, 2019. [ arXiv | http ]
  • Hugo Verhelst. Modelling wrinkling behaviour of large floating thin offshore structures: An application of isogeometric structural analysis for post-buckling analyses, 2019. [ http ]
  • Jochen Hinz, Matthias Möller, and Cornelis Vuik. Spline-based parameterization techniques for twin-screw machine geometries. IOP Conference Series: Materials Science and Engineering, 425:012030, nov 2018. (pdf). [ DOI | http ]
  • Jochen Hinz, Matthias Möller, and Cornelis Vuik. Elliptic grid generation techniques in the framework of isogeometric analysis applications. Computer Aided Geometric Design, 65:48--75, oct 2018. [ DOI | http ]
  • Jochen Hinz, Matthias Möller, and Cornelis Vuik. Spline-based meshing techniques for industrial applications. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) and the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, jun 2018. ECCOMAS. (pdf).
  • Jochen Hinz, Matthias Möller, and Cornelis Vuik. An IGA framework for PDE-based planar parameterization on convex multipatch domains. In Harald van Brummelen, Kees Vuik, Matthias Möller, Clemens Verhoosel, Bernd Simeon, and Bert Jüttler, editors, Proceedings of the 3rd Conference on Isogeometric Analysis and Applications (IGAA 2018), 2020. [ arXiv | http ]
  • Matthias Möller and Jochen Hinz. Isogeometric analysis framework for the numerical simulation of rotary screw machines. I. General concept and early applications. IOP Conference Series: Materials Science and Engineering, 425:012032, nov 2018. [ DOI | http ]
  • Matthias Möller and Andrzej Jaeschke. FDBB: Fluid dynamics building blocks. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) and the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, jun 2018. ECCOMAS. (pdf). [ arXiv | http ]
  • Roel Tielen, Matthias Möller, and Cornelis Vuik. Efficient p-multigrid based solvers for multipatch geometries in isogeometric analysis. In Harald van Brummelen, Kees Vuik, Matthias Möller, Clemens Verhoosel, Bernd Simeon, and Bert Jüttler, editors, Proceedings of the 3rd Conference on Isogeometric Analysis and Applications (IGAA 2018), 2018. [ .pdf ]
  • Roel Tielen, Matthias Möller, and Cornelis Vuik. Efficient multigrid based solvers for isogeometric analysis. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) and the 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, jun 2018. ECCOMAS. (pdf).
  • Kenny David. Multi-patch discontinuous Galerkin isogeometric analysis for porous media flow, 2017. [ http ]
  • Jochen Hinz. Isogeometric analysis of a reaction-diffusion model for human brain development, 2016. [ http ]
FEM
  • Jie Liu, Matthias Möller, and Henk M. Schuttelaars. Balancing truncation and round-off errors in FEM: One-dimensional analysis, 2021. [ DOI | arXiv | http ]
  • Jakob M. Maljaars, Robert Jan Labeur, and Matthias Möller. A hybridized discontinuous Galerkin framework for high-order particle-mesh operator splitting of the incompressible Navier-Stokes equations. Journal of Computational Physics, 358:150--172, apr 2018. [ DOI | http ]
  • Jakob Maljaars, Robert Jan Labeur, Matthias Möller, and Wim Uijttewaal. Development of a hybrid particle-mesh method for simulating free-surface flows. Journal of Hydrodynamics, 29(3):413--422, jun 2017. [ DOI | http ]
  • Jakob Maljaars, Robert J. Labeur, Matthias Möller, and Wim Uijttewaal. A numerical wave tank using a hybrid particle-mesh approach. Procedia Engineering, 175:21--28, 2017. [ DOI | http ]
  • Jakob M. Maljaars. A hybrid particle-mesh method for simulating free surface flows, 2016. [ http ]
  • Dominik Göddeke, Dimitri Komatitsch, and Matthias Möller. Finite and spectral element methods on unstructured grids for flow and wave propagation problems. In Numerical Computations with GPUs, pages 183--206. Springer International Publishing, 2014. [ DOI | http ]
  • Dmitri Kuzmin, Matthias Möller, and Marcel Gurris. Algebraic flux correction II. In Flux-Corrected Transport, pages 193--238. Springer Netherlands, 2012. (pdf). [ DOI | http ]
  • Matthias Möller. On the design of non-conforming high-resolution finite element schemes. In Proceedings of the 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012). ECCOMAS, 2012. [ .pdf ]
  • Dmitri Kuzmin, Matthias Möller, John N. Shadid, and Mikhail Shashkov. Failsafe flux limiting and constrained data projections for equations of gas dynamics. Journal of Computational Physics, 229(23):8766--8779, nov 2010. (pdf). [ DOI | http ]
  • Dmitri Kuzmin and Matthias Möller. Goal-oriented mesh adaptation for flux-limited approximations to steady hyperbolic problems. Journal of Computational and Applied Mathematics, 233(12):3113--3120, apr 2010. (pdf). [ DOI | http ]
  • Matthias Möller. Adaptive high-resolution finite element schemes, 2008. [ .pdf ]
  • Matthias Möller and Dmitri Kuzmin. Adaptive mesh refinement for high-resolution finite element schemes. International Journal for Numerical Methods in Fluids, 52(5):545--569, 2006. (pdf). [ DOI | http ]